在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针 旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.
今年是中华人民共和国建国70周年,襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动.学校3000名学生全部参加了竞赛,结果所有学生成绩都不低于60分(满分100分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表.根据表中所给信息,解答下列问题:
|
成绩 (分 分组 |
频数 |
频率 |
|
|
15 |
0.30 |
|
|
|
0.40 |
|
|
10 |
|
|
|
5 |
0.10 |
(1)表中 , ;
(2)这组数据的中位数落在 范围内;
(3)判断:这组数据的众数一定落在 范围内,这个说法 (填“正确”或“错误” ;
(4)这组数据用扇形统计图表示,成绩在 范围内的扇形圆心角的大小为 ;
(5)若成绩不小于80分为优秀,则全校大约有 名学生获得优秀成绩.
先化简,再求值: ,其中 .
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 , 两点且与 轴的负半轴交于点 .
(1)求该抛物线的解析式;
(2)若点 为直线 上方抛物线上的一个动点,当 时,求点 的坐标;
(3)已知 , 分别是直线 和抛物线上的动点,当以 , , , 为顶点的四边形是平行四边形时,直接写出所有符合条件的 点的坐标.

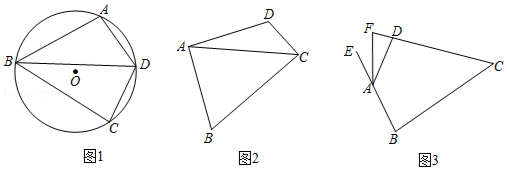
定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点 , , 在 上, 的平分线交 于点 ,连接 , .
求证:四边形 是等补四边形;
探究:
(2)如图2,在等补四边形 中, ,连接 , 是否平分 ?请说明理由.
运用:
(3)如图3,在等补四边形 中, ,其外角 的平分线交 的延长线于点 , , ,求 的长.
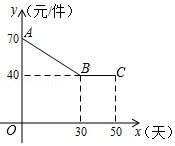
某工厂用50天时间生产一款新型节能产品,每天生产的该产品被某网店以每件80元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第 天的生产成本 (元 件)与 (天 之间的关系如图所示,第 天该产品的生产量 (件 与 (天 满足关系式 .
(1)第40天,该厂生产该产品的利润是 元;
(2)设第 天该厂生产该产品的利润为 元.
①求 与 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于2400元的共有多少天?