(本小题满分16分)
已知数列 满足
满足 ,当
,当 ,
, 时,
时, .
.
⑴求数列 的通项公式;
的通项公式;
⑵是否存在 ,使得
,使得 时,不等式
时,不等式 对任意实数
对任意实数 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
⑶在 轴上是否存在定点
轴上是否存在定点 ,使得三点
,使得三点 、
、 、
、 (其中
(其中 、
、 、
、 是互不相等的正整数且
是互不相等的正整数且 )到定点
)到定点 的距离相等?若存在,求出点
的距离相等?若存在,求出点 及正整数
及正整数 、
、 、
、 ;若不存在,说明理由.
;若不存在,说明理由.
有一种舞台灯,外形是正六棱柱ABCDEF—A1B1C1D1E1F1,在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯,假若每只灯正常发光的概率是0.5,若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面. 假定更换一个面需100元,用ξ表示维修一次的费用.
(1)求面ABB1A1需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
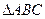 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为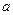 、
、 、
、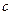 ,若
,若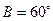 ,
, 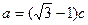 .
.
(1)求角 的大小;
的大小;
(2)已知 ,求函数
,求函数 的最大值
的最大值
已知函数f(x)=x3-ax-b (a,b∈R)
(1)当a=b=1时,求函数f(x)的单调区间
(2)是否存在a,b,使得 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
如图,已知直线 的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线
的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线 上的射影依次为点D,K,E.
上的射影依次为点D,K,E.
(1)若抛物线 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)连接AE,BD,证明:当m变化时,直线AE、BD相交于一定点。
已知函数 .
.
(1)当 时,函数
时,函数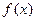 取得极大值,求实数
取得极大值,求实数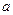 的值;
的值;
(2)若存在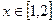 ,使不等式
,使不等式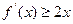 成立,其中
成立,其中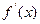 为
为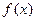 的导函数,求实数
的导函数,求实数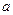 的取值范围;
的取值范围;
(3)求函数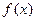 的单调区间。
的单调区间。