(本小题满分12分) 已知椭圆C的对称中心为原点O，焦点在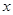
轴上，离心率为
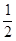，且过点
．
（1）求椭圆C的方程；
（2） 过椭圆C的左焦点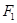
的直线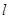
与椭圆C相交于
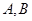两点，若
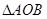的面积为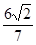
，求圆心在原点O且与直线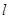相切的圆的方程．
已知命题p：正方形的两条对角线互相垂直；命题q：正方形的两条对角线相等，写出命题 “p或q”“p且q”“非p”，并指出真假．
分别指出由下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题的真假：
（1）p：方程x2+1=0有实数根；q：方程x2－1=0的两根相等．
（2）p：等腰三角形两底角相等；q：等腰三角形为锐角三角形．
指出下列复合命题的形式，：
（1）ｘ＝２和ｘ＝３是方程ｘ２－５ｘ＋６＝０的根；
（2）x2－3x+2＜0，则1＜x＜2；
（3）ｘ＋１≥ｘ－３；
（4）1既不是质数，也不是合数；
(12分)指出下列数学式子的确切含义：
(1)“a≥b”； (2)“a＝±b”； (3)“a≠±b”．
已知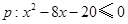
，
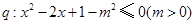．若
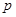是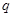
的必要不充分条件，求实数
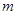的取值范围 ．