(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的 ,总有
,总有 成立,求常数
成立,求常数 的值;
的值;
(2)在数列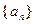 中,
中,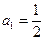 ,
,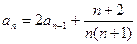 (
( ,
, ),求通项
),求通项 ;
;
(3)在(2)题的条件下,设 ,从数列
,从数列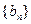 中依次取出第
中依次取出第 项,第
项,第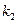 项,…第
项,…第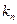 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列 ,其中
,其中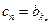 ,其中
,其中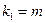 ,
, .试问是否存在正整数
.试问是否存在正整数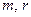 使
使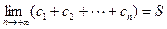 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数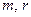 的值;不存在,说明理由.
的值;不存在,说明理由.
设函数 (Ⅰ)若函数
(Ⅰ)若函数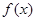 在
在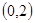 上单调递减,在区间
上单调递减,在区间 单调递增,求
单调递增,求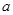 的值;
的值;
(Ⅱ)若函数 在
在 上有两个不同的极值点,求
上有两个不同的极值点,求 的取值范围;
的取值范围;
(Ⅲ)若方程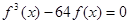 有且只有三个不同的实根,求
有且只有三个不同的实根,求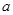 的取值范围。
的取值范围。
已知数列 的前n项和为
的前n项和为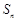 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,数列
,数列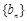 的前n项和为
的前n项和为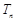 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图 ,在直角梯形
,在直角梯形 中,
中, ,
, ∥
∥ ,
,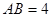 ,
, ,将
,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(Ⅰ)求证: 平面
平面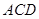 ;
;
(Ⅱ)求几何体 的体积.
的体积.
某同学参加省学业水平测试,物理、化学、生物获得等级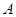 和获得等级不是
和获得等级不是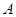 的机会相等,物理、化学、生物获得等级
的机会相等,物理、化学、生物获得等级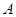 的事件分别记为
的事件分别记为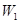 、
、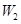 、
、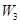 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是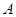 的事件分别记为
的事件分别记为 、
、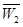 、
、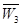 .
.
(Ⅰ)试列举该同学这次水平测试中物理、化学、生物成绩是否为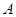 的所有可能结果(如三科成绩均为
的所有可能结果(如三科成绩均为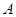 记为
记为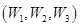 );
);
(Ⅱ)求该同学参加这次水平测试获得两个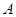 的概率;
的概率;
(Ⅲ)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于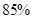 ,并说明理由.
,并说明理由.
已知向量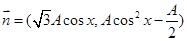 ,
,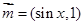 ,
,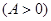 ,函数
,函数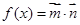 的最大值为
的最大值为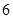 .
.
(Ⅰ)求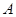 ;
;
(Ⅱ)将函数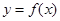 的图像向左平移
的图像向左平移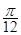 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的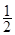 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数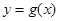 的图像,求
的图像,求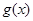 在
在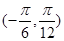 上的值域.
上的值域.