已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
(Ⅰ)求正三棱柱的侧棱长.
(Ⅱ)若M为BC1的中点,试用基底向量 、
、 、
、 表示向量
表示向量 ;
;
(Ⅲ)求异面直线AB1与BC所成角的余弦值.
在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
(1)求角 的值;
的值;
(2)若 且
且 ,求
,求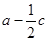 的取值范围.
的取值范围.
(本小题满分14分)已知函数 ,
,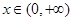 ,
, .
.
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)若对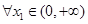 ,总存在
,总存在 使得
使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)证明不等式: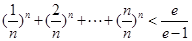 .
.
(本小题满分15分)等比数列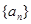 的前
的前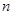 项和
项和 ,已知
,已知 ,
, ,
,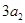 ,
, 成等差数列.
成等差数列.
(Ⅰ)求数列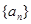 的公比
的公比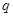 和通项
和通项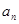 ;
;
(Ⅱ)若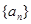 是递增数列,令
是递增数列,令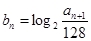 ,求
,求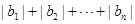 .
.
(本小题满分15分)如图甲, 是边长为6的等边三角形,
是边长为6的等边三角形, ,
, 分别为
分别为 、
、 靠近
靠近 、
、 的三等分点,点
的三等分点,点 为
为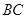 边的中点.线段
边的中点.线段 交线段
交线段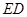 于
于 点,将
点,将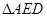 沿
沿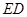 翻折,使平面
翻折,使平面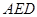 ⊥平面
⊥平面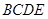 ,连接
,连接 、
、 、
、 形成如图乙所示的几何体.
形成如图乙所示的几何体.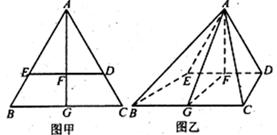
(Ⅰ)求证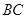 ⊥平面
⊥平面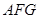 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分15分)己知函数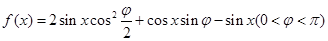 在
在 处取最小值.
处取最小值.
(Ⅰ)求 的值.
的值.
(Ⅱ)在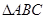 中,
中, 、
、 、
、 分别是
分别是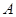 、
、 、
、 的对边,已知
的对边,已知 ,
,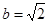 ,
,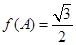 ,求角
,求角 .
.