在△ABC中,已知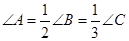 ,它的最长边是8cm,求它的最短边的长。
,它的最长边是8cm,求它的最短边的长。
在解一元二次方程时,粗心的甲、乙两位同学分别抄错了同一道题,甲抄错了常数项,得到的两根分别是8和2;乙抄错了一次项系数,得到的两根分别是-9和-1.你能找出正确的原方程吗?若能,请你用配方法求出这个方程的根.
如图,某农户为了发展养殖业,准备利用一段墙( 墙长18米)和55米长的竹篱笆围成三个相连且面积相等的长方形鸡、鸭、鹅各一个.问:( 1)如果鸡、鸭、鹅场总面积为150米2,那么有几种围法?(2)如果需要围成的养殖场的面积尽可能大,那么又应怎样围,最大面积是多少?
某商场今年1月份销售额为100万元,2月份销售额下降了10%, 该商场马上采取措施,改进经营管理,使月销售额大幅上升,4月份的销售额达到129.6万元,求3, 4月份平均每月销售额增长的百分率.
某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,求这个百分数.
已知关于x的一元二次方程x2-2kx+ k2-2=0.
k2-2=0.
(1)求证:不论k为何值,方程总有两不相等实数根.
(2)设x1,x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.