(本小题满分12分)
已知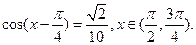
(1)求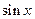 的值;
的值;
(2)求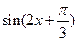 的值.
的值.
(本小题满分10分)
在 中,角
中,角 所对的边分别是
所对的边分别是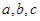 ,且满足
,且满足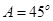 ,
,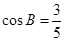 .
.
(Ⅰ)求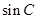 的值;
的值;
(Ⅱ)设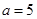 ,求
,求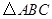 的面积.
的面积.
已知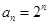 ,把数列
,把数列 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记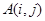 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论
① ;
;
②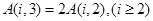 ;
;
③ ;
;
④ .
.
其中正确的是__________ (写出所有正确结论的序号).
(本小题满分14分)
已知二次函数 满足以下两个条件:
满足以下两个条件:
①不等式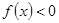 的解集是(-2,0)②函数
的解集是(-2,0)②函数 在
在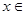
 上的最小值是3
上的最小值是3
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若点
 在函数
在函数 的图象上,且
的图象上,且
(ⅰ)求证:数列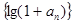 为等比数列
为等比数列
(ⅱ)令 ,是否存在正实数
,是否存在正实数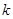 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立?若存在,指出
恒成立?若存在,指出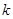 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.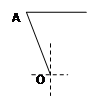
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行时间应为多少小时?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(本小题满分12分)如图所示,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区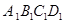 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区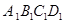 的面积为4000 m 2,人行道的宽分别为4 m和10 m.
的面积为4000 m 2,人行道的宽分别为4 m和10 m.
( I )设休闲区的长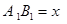 m ,求公园ABCD所占面积
m ,求公园ABCD所占面积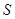 关于 x 的函数
关于 x 的函数 的解析式;
的解析式;
(Ⅱ)要使公园ABCD所占总面积最小,休闲区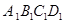 的长和宽该如何设计?
的长和宽该如何设计?