(本题14分)某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 |
二月 |
三月 |
四月 |
五月 |
六月 |
| 2010 |
2.7 |
2.4 |
2.8 |
3.1 |
2.9 |
| 2011 |
4.9 |
5.0 |
x |
y |
z |
在平面直角坐标系中,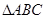 各顶点的坐标分别为:
各顶点的坐标分别为: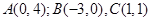
(1)求点C到直线AB的距离;
(2)求AB边的高所在直线的方程.
(本小题满分12分)已知直线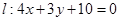 ,半径为
,半径为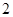 的圆
的圆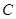 与
与 相切,圆心
相切,圆心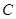 在
在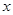 轴上且在直线
轴上且在直线 的上方
的上方
(1)求圆 的方程;
的方程;
(2)过点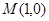 的直线与圆
的直线与圆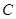 交于
交于 两点(
两点(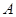 在
在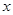 轴上方),问在
轴上方),问在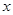 轴正半轴上是否存在点
轴正半轴上是否存在点 ,使得
,使得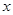 轴平分
轴平分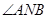 ?若存在,请求出点
?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)平面 平面
平面 ,
, 为正方形,
为正方形,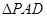 是直角三角形,且
是直角三角形,且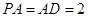 ,
,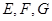 分别是线段
分别是线段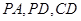 的中点
的中点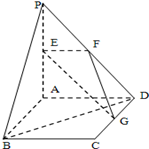
(1)求证: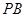 //平面
//平面 ;
;
(2)在线段 上是否存在一点
上是否存在一点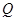 ,使得点
,使得点 到平面
到平面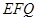 的距离为
的距离为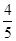 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)(理科)已知圆
(1)若圆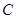 的切线在
的切线在 轴和
轴和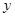 轴上截距相等,求切线的方程;
轴上截距相等,求切线的方程;
(2)从圆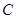 外一点
外一点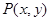 向圆引切线
向圆引切线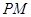 ,
,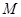 为切点,
为切点, 为坐标原点,且
为坐标原点,且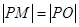 ,求
,求 的最小值
的最小值
(本小题满分12分)在如图所示的几何体中,四边形 是正方形,
是正方形,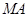
 平面
平面 ,
,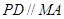 ,
, 、
、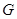 、
、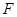 分别为
分别为 、
、 、
、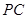 的中点,且
的中点,且 .
.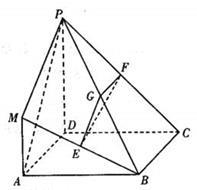
(1)求证:平面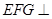 平面
平面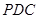 ;
;
(2)若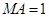 ,求四棱锥
,求四棱锥 的体积.
的体积.