(本题12分)某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.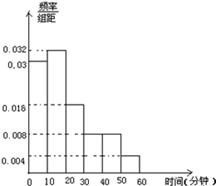
(1)若抽取的50个样本是用系统抽样的方法得到,
且第一段的号码为006,则第五段抽取的号码是什么?
(2)若从50个样本中属于第4组和第6组的所有人
中随机抽取2人,设他们上学时间分别为a、b,求满足
|a-b|>10的事件的概率;
(3)设学校配备的校车每辆可搭载40名学生,请根
据抽样的结果估计全校应有多少辆这样的校车?
设M点的坐标为(x,y).
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中取随机取一个数作为y,求M点落在y轴的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组:
,所表示的平面区域内的概率
投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机散一粒豆子,求豆子落在区域M上的概率.
设an=1+q+q2+…+qn-1,An=Ca1+Ca2+…+Can.
(1)用q和n表示An;
(2)又设b1+b2+…+bn=.求证:数列是等比数列.
若(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11.求:
(1)a1+a2+a3+…+a11;
(2)a0+a2+a4+…+a10.
在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
(1)求它是第几项;
(2)求的范围.