设数列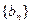 满足:
满足: ,
,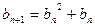 ,
,
(1)求证: ;
;
(2)若 ,对任意的正整数
,对任意的正整数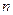 ,
,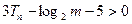 恒成立.求m的取值范围.
恒成立.求m的取值范围.
(本小题满分10分)选修:4-4:坐标系与参数方程
已知:圆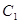 的参数方程为
的参数方程为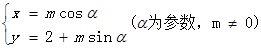 ,圆
,圆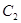 的极坐标方程为
的极坐标方程为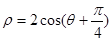 ,
,
(1)求圆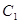 的普通方程与圆
的普通方程与圆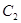 的直角坐标方程;
的直角坐标方程;
(2)若圆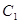 与圆
与圆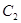 外切,求实数
外切,求实数 的值;
的值;
(本小题满分10分)选修4-1:几何证明选讲
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明: AD·DE=2PB2.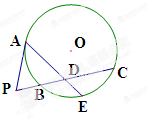
已知函数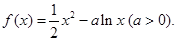
(Ⅰ)若函数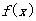 在
在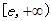 上位增函数,求
上位增函数,求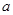 的取值范围.
的取值范围.
(Ⅱ) 求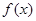 在区间
在区间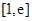 上的最小值;
上的最小值;
(Ⅲ) 若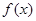 在区间
在区间 上恰有两个零点,求
上恰有两个零点,求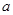 的取值范围.
的取值范围.
已知椭圆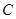 :
: 的离心率为
的离心率为 ,右顶点
,右顶点 是抛物线
是抛物线 的焦点.直线
的焦点.直线 :
: 与椭圆
与椭圆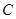 相交于
相交于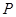 ,
, 两点.
两点.
(Ⅰ)求椭圆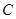 的方程;
的方程;
(Ⅱ)如果 ,点
,点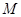 关于直线
关于直线 的对称点
的对称点 在
在 轴上,求
轴上,求 的值.
的值.
如图,在四棱锥P—ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD =" CD" =" 2AB" = 2,E为PC的中点,DE = EC
(1)求证: 平面
平面
(2)设PA = a,若平面EBD与平面ABCD所成锐二面角的为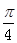 ,求a的值。
,求a的值。