如图,在四棱锥P—ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD =" CD" =" 2AB" = 2,E为PC的中点,DE = EC
(1)求证: 平面
平面
(2)设PA = a,若平面EBD与平面ABCD所成锐二面角的为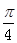 ,求a的值。
,求a的值。
已知复数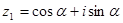 ,
, 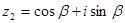 ,
, 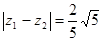 ,求:(1)求
,求:(1)求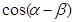 的值;(2)若
的值;(2)若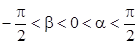 ,且
,且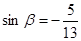 ,求
,求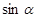 的值.
的值.
如图,抛物线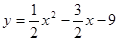 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合)。过点E作直线l平行BC,交AC于点D。设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留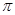 )。
)。
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.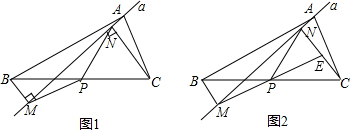
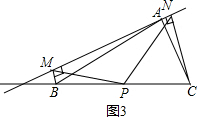
(1)延长MP交CN于点E(如图2).
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
| 型号 |
A |
B |
| 成本(万元/台) |
200 |
240 |
| 售价(万元/台) |
250 |
300 |
(1该厂对这两种型号挖掘机有几种生产方案?
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高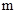 万元(
万元(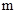 >0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
| 运输工具 |
运输费单价:元/(吨•千米) |
冷藏费单价:元/(吨•时) |
固定费用:元/次 |
| 汽车 |
2 |
5 |
200 |
| 火车 |
1.6 |
5 |
2280 |
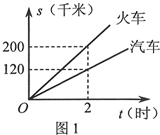

(1)汽车的速度为千米/时,火车的速度为千米/时:
(2)设每天用汽车和火车运输的总费用分别为 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与  的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?