已知A、B两地的路程为240千米．某经销商每天都要用汽车或火车将吨保鲜品一次 性由A地运往B地．受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订．
现有货运收费项目及收费标准表、行驶路程s（千米）与行驶时间t（时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：
货运收费项目及收费标准表

运输工具	运输费单价：元/（吨•千米）	冷藏费单价：元/（吨•时）	固定费用：元/次
汽车	2	5	200
火车	1.6	5	2280

          
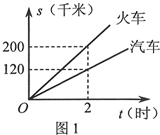
（1）汽车的速度为       千米/时，火车的速度为       千米/时：
（2）设每天用汽车和火车运输的总费用分别为_汽（元）和_火（元），分别求_汽、_火与 的函数关系式（不必写出的取值范围），及为何值时_汽＞_火（总费用=运输费+冷藏费+固定费用）
（3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？

科目 数学   题型 解答题   难度 较易