某工程机械厂根据市场要求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22400万元，但不超过22500万元，且所筹资金全部用于生产这两种型号的挖掘机，所生产的这两种型号的挖掘机可全部售出，此两种型号挖掘机的生产成本和售价如下表所示：
| 型号 |
A |
B |
| 成本（万元/台） |
200 |
240 |
| 售价（万元/台） |
250 |
300 |
（1该厂对这两种型号挖掘机有几种生产方案？
（2）该厂如何生产获得最大利润？
（3）根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高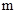
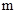万元（>0），该厂如何生产可以获得最大利润？（注：利润=售价-成本）
(本小题满分12分)已知直三棱柱
中，
，
为
中点，
为
中点，侧面
为正方形。
(1)证明：
平面
；
(2)证明：
；
(本小题满分12分) 已知直线
经过直线
与直线
的交点
，且垂直于直线
.
（1）求直线的方程；
（2）求直线与两坐标轴围成的三角形的面积
.
（本小题满分16分）已知椭圆
：
的离心率为
，直线
：
与椭圆相切．
（1）求椭圆的方程；
（2）设椭圆的左焦点为
，右焦点为
，直线
过点且垂直与椭圆的长轴，动直线
垂直于直线于点
，线段
的垂直平分线交于点
，求点的轨迹
的方程.
（本小题满分16分）如图，平面直角坐标系
中，
和
为等腰直角三角形，
,
设和的外接圆圆心分别为
.
（Ⅰ）若圆M与直线
相切，求直线的方程；
（Ⅱ）若直线
截圆N所得弦长为4，求圆N的标准方程；
（Ⅲ）是否存在这样的圆N，使得圆N上有且只有三个点到直线的距离为
，若存在，求此时圆N的标准方程；若不存在，说明理由.
（本小题满分15分） 设
．
（1）求函数
的单调递增、递减区间；
（2）求函数在区间
上的最大值和最小值．