(本题满分12分) 已知函数 为
为 上的连续函数
上的连续函数
(Ⅰ) 若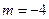 ,判断
,判断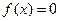 在
在 上是否有零根存在?没有,请说明理由;若有,并在精确度为
上是否有零根存在?没有,请说明理由;若有,并在精确度为 的条件下(即根所在区间长度小于
的条件下(即根所在区间长度小于 ),用二分法求出使这个零根
),用二分法求出使这个零根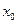 存在的小区间;
存在的小区间;
(Ⅱ)若函数 在区间
在区间 上存在零点,求实数
上存在零点,求实数 的取值范围.
的取值范围.
(本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为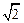 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
(本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,
前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明: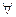 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(本题满分14分) 设向量α=(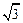 sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f(x)=α
sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f(x)=α β.
β.
(Ⅰ) 求f(x)的最小正周期;
(Ⅱ) 若f(θ)=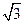 ,其中0<θ<
,其中0<θ<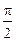 ,求cos(θ+
,求cos(θ+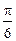 )的值.
)的值.
已知函数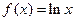 ,
,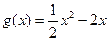
(1) 设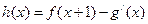 (其中
(其中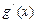 是
是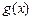 的导函数),求
的导函数),求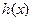 的最大值;
的最大值;
(2) 证明: 当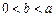 时,求证:
时,求证: ;
;
(3) 设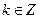 ,当
,当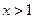 时,不等式
时,不等式 恒成立,求
恒成立,求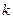 的最大值
的最大值
在数列 中,
中,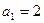 ,
, ,且已知函数
,且已知函数 在
在 处取得极值。
处取得极值。
⑴证明:数列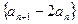 是等比数列
是等比数列
⑵求数列 的通项
的通项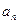 和前
和前 项和
项和