某化妆品公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):
(1)求y1的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好?至少要销售商品多少件?
如图,在梯形ABCD中,AD//BC,AB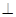 AD,对角线BD
AD,对角线BD 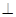 DC,
DC,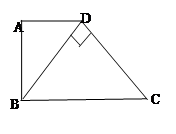
(1)试说明:ΔABD∽ΔDCB;
(2)若BD=7,AD=5,求BC的长。
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为(,);
依此类推第n条抛物线yn的顶点坐标为(,);
所有抛物线的顶点坐标满足的函数关系是;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.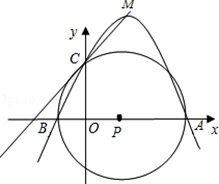
(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
如图1,有一组平行线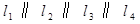 ,正方形
,正方形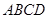 的四个顶点分别在
的四个顶点分别在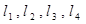 上,
上,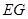 过点D且垂直于
过点D且垂直于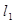 于点E,分别交
于点E,分别交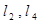 于点F,G,
于点F,G,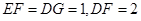 .
.
(1)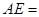 ,正方形
,正方形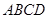 的边长=;
的边长=;
(2)如图2,将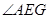 绕点A顺时针旋转得到
绕点A顺时针旋转得到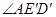 ,旋转角为
,旋转角为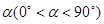 ,点
,点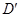 在直线
在直线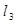 上,以
上,以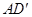 为边在的
为边在的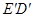 左侧作菱形
左侧作菱形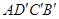 ,使点
,使点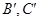 分别在直线
分别在直线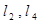 上.
上.
①写出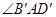 与
与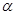 的函数关系并给出证明;②若
的函数关系并给出证明;②若 ,求菱形
,求菱形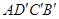 的边长.
的边长.
如图所示,在Rt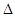 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为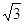 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt ABC顺时针旋转120
ABC顺时针旋转120 后得到Rt
后得到Rt ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.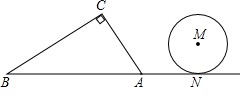
(1)画出旋转后的Rt ADE;
ADE;
(2)求出Rt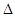 ADE的直角边DE被⊙M截得的弦PQ的长度;
ADE的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt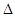 ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.