(本小题满分12分)由于当前学生课业负担较重,造成青少年视力普遍下降,现从湖口中学随机抽取16名学生,经校医用对数视力表检查得到每 个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,求校医从这16人中随机选取3人,至多有1人是“good sight”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记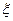 表示抽到“good sight”学生的人数,求
表示抽到“good sight”学生的人数,求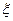 的分布列及数学期望.
的分布列及数学期望.
在等腰梯形ABCD中, ,
,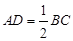 ,
, ,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转
,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转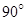 ,得到梯形
,得到梯形 .
.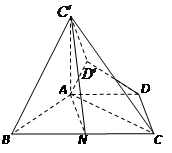
(1)求证: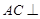 平面
平面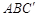 ;
;
(2)求证: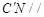 平面
平面 ;
;
已知数列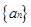 的前
的前 项和为
项和为 ,且满足:
,且满足: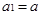
 ,
,
 N*,
N*,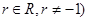 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若存在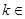 N*,使得
N*,使得 ,
,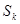 ,
, 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的 N*,且
N*,且 ,
, ,
, ,
,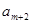 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.
设函数 (1)求
(1)求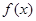 的单调递增区间. (2)已知函数
的单调递增区间. (2)已知函数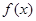 的图象在点A(
的图象在点A(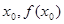 )处,切线斜率为
)处,切线斜率为 ,求:
,求: 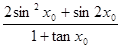
已知函数f(x)=aln x-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2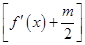 (f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: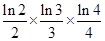 ×…×
×…× <
< (n≥2,n∈N*).
(n≥2,n∈N*).
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于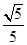 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.