(本小题满分13分)
某学生在上学路上要经过4个路口，假设在
各路口是否遇到红灯是相互独立的，遇到红灯的概率都是
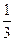，遇到红灯时停留的时间都是2min.
（Ⅰ）求这名学生在上学路上到第三个路口时首次遇到红灯的概率；
（Ⅱ）求这名学生在上学路上因遇到红灯停留的总时间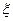
的分布列及期望.
（本小题满分13分）如图，在四棱锥PABCD中，侧面PAD⊥底面ABCD，侧棱
，
，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，O为AD中点．
（Ⅰ）求证：
平面
；
（Ⅱ）求直线
与平面
所成角的大小；
已知函数
（Ⅰ）求
的单调增区间；
（Ⅱ）若
，求的最大值和最小值．
若数列
的各项均为正数，
，
为常数，且
.
（1）求
的值；
（2）证明：数列为等差数列；
（3）若
，对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使
，
，
成等差数列？若存在，用k分别表示一组p和r；若不存在，请说明理由．
函数
．
（1）若
，求曲线
在
的切线方程；
（2）若函数
在
上是增函数，求实数
的取值范围；
（3）设点
，
，
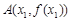满足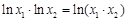
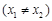，判断是否存在实数，使得
为直角？说明理由．
已知
的三个顶点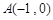
，
，
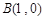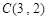，其外接圆为圆
．
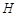（1）求圆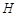的方程；
（2）若直线
过点
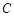，且被圆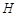截得的弦长为2，求直线的方程；
（3）对于线段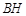
上的任意一点
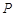，若在以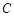为圆心的圆上都存在不同的两点
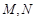，使得点
是线段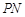
的中点，求圆
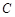的半径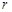
的取值范围．