(本小题满分13分)
已知椭圆 过点
过点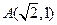 ,且点
,且点 在
在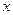 轴上的射影恰为椭圆的一个焦点
轴上的射影恰为椭圆的一个焦点
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过 作两条倾斜角互补的直线与椭圆分别交于
作两条倾斜角互补的直线与椭圆分别交于 两点.试问:四边形
两点.试问:四边形 能否为平行四边形?若能,求出直线
能否为平行四边形?若能,求出直线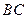 的方程;否则说明理由.
的方程;否则说明理由.
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是 (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: .今有
.今有 万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
已知 .
.
(1) ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
如图,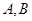 是椭圆
是椭圆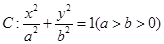 的左右顶点,
的左右顶点,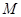 是椭圆上异于
是椭圆上异于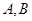 的任意一点,若椭圆
的任意一点,若椭圆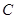 的离心率为
的离心率为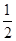 ,且右准线
,且右准线 的方程为
的方程为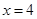
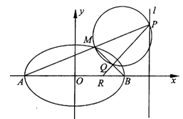
(1)求椭圆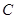 的方程;
的方程;
(2)设直线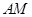 交
交 于点
于点 ,以
,以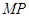 为直径的圆交直线
为直径的圆交直线 于点
于点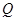 ,试证明:直线
,试证明:直线 与
与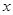 轴的交点
轴的交点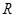 为定点,并求出
为定点,并求出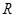 点的坐标.
点的坐标.
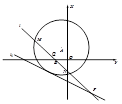
如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点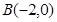 的动直线
的动直线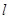 与圆
与圆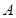 相交于
相交于 两点,
两点,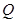 是
是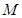 的中点,直线
的中点,直线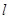 与
与 相交于点
相交于点 .
.
(1)求圆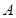 的方程;
的方程;
(2)当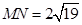 时,求直线
时,求直线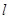 的方程;
的方程;
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
已知圆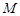 :
: ,设点
,设点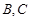 是直线
是直线 :
: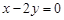 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点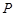 在线段
在线段 上,过
上,过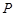 点作圆
点作圆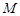 的切线
的切线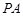 ,切点为
,切点为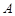 .
.
(1)若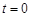 ,
,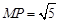 ,求直线
,求直线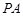 的方程;
的方程;
(2)若O为原点,经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 长的最小值
长的最小值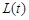 .
.