(本小题满分14分)
本题是选作题，考生只能选做其中两个小题．三个小题都作答的，以前两个小题计算得分。
①选修4－4《坐标系与参数方程》选做题（本小题满分7分）
已知曲线C的参数方程是
为参数)，且曲线C与直线
=0相交于两点A、B求弦AB的长。
②选修4－2《矩阵与变换》选做题（本小题满分7分）
已知矩阵
的一个特征值为
,它对应的一个特征向量
。
（Ⅰ）求矩阵M；
（Ⅱ）点P(1, 1)经过矩阵M所对应的变换,得到点Q，求点Q的坐标。
③选修4－5《不等式选讲》选做题（本小题满分7分）
函数
的图象恒过定点
,若点在直
线
上,其中
,求
的最小值。
M公司从某大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分），公司规定：成绩在180分以上者到“甲部门”工作；180分以下者到“乙部门”工作。
（I）求男生成绩的中位数及女生成绩的平均值；
（II）如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人，再从这5人中选2人，那么至少有一人是“甲部门”人选的概率是多少？
如图，五面体中，四边形ABCD是矩形，DA
面ABEF，且DA=1，AB//EF，
，P、Q、M分别为AE、BD、EF的中点.
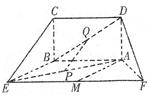
求证：（I）PQ//平面BCE；
（II）求证：AM平面ADF；
设数列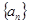
为等差数列，且
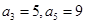；数列
的前n项和为
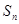，且
。
（I）求数列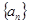，的通项公式；
（II）若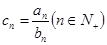
，
为数列
的前n项和，求。
已知函数
的最小正周期为
.
（I）求函数
的对称轴方程；
（II）若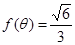
，求
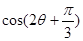的值.
（本小题满分12分）已知函数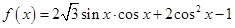
．
（Ⅰ）求函数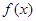
的单调递增区间；
（Ⅱ）若关于
的方程
在区间
上有两个不同的实数根，求实数
的取值范围．