(本小题满分12分)
 为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第
为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第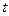 小时教室内每立方米空气中的含药量为
小时教室内每立方米空气中的含药量为 毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为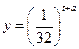 (a为常数).函数图象如图所示.
(a为常数).函数图象如图所示.
根据图中提供的信息,解答下列问题:
(1)求从药物释放开始每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
|
(2)按规定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间,学生才能回到教室?

某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数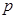 与听课时间
与听课时间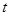 之间的关系满足如图所示的曲线。当
之间的关系满足如图所示的曲线。当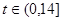 时,曲线是二次函数图象的一部分,其中对称轴为
时,曲线是二次函数图象的一部分,其中对称轴为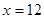 ;当
;当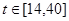 时,曲线是函数
时,曲线是函数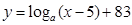
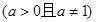 图象的一部分。根据专家研究,当注意力指数
图象的一部分。根据专家研究,当注意力指数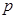 大于或等于80时听课效果最佳.
大于或等于80时听课效果最佳.
(1)试求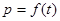 的函数关系式;
的函数关系式;
(2)老师在什么时间段内安排核心内容能使学生听课效果最佳?请说明理由.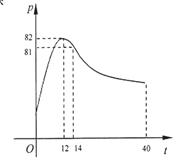
已知函数 (
(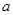 为实常数)
为实常数)
(1)若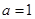 ,求
,求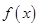 的单调区间;
的单调区间;
(2)若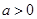 ,设
,设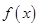 在区间
在区间 的最小值为
的最小值为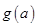 ,求
,求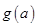 的表达式.
的表达式.
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:
5 6 7 8 9 10
把这6名学生的得分看成一个总体.
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样的方法从6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率
已知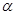 是三角形的内角,且
是三角形的内角,且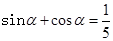
(Ⅰ)求 的值;
的值;
(Ⅱ)把 用
用 表示出来,并求其值
表示出来,并求其值
为了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如上图),图中从左到右各小长方形面积之比为2: 4: 17: 15: 9: 3,第二小组的频数为12.
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计学校全体高一学生的达标率是多少?