如图,等边
与直角梯形
垂直,
,
,
,
.若
分别为
的中点.
（1）求
的值； （2）求面
与面
所成的二面角大小.
某单位从一所学校招收某类特殊人才．对
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试，其测试结果如下表：
例如，表中运动协调能力良好且逻辑思维能力一般的学生有
人．由于部分数据丢失，只知道从这位参加测试的学生中随机抽取一位，抽到运动协调能力或逻辑思维能力优秀的学生的概率为
．
（1）求
，
的值；
（2）从参加测试的位学生中任意抽取
位，求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率；
（3）从参加测试的位学生中任意抽取位，设运动协调能力或逻辑思维能力优秀的学生人数为
，求随机变量的分布列及其数学期望
．
已知函数
，
．
（1）求
的值及函数
的最小正周期；
（2）求函数在
上的单调减区间．
已知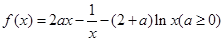
（1）当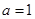
时，求
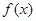的极值；
（2）当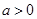
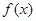时，讨论的单调性；
（3）若对任意的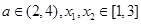
,恒有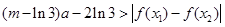
成立，求实数
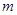的取值范围.
已知椭圆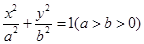
的由顶点为A，右焦点为F，直线
与x轴交于点B且与直线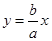
交于点C，点O为坐标原点，
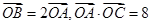,过点F的直线
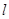与椭圆交于不同的两点M,N.
（1）求椭圆的方程；
（2）求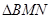
的面积的最大值.
数列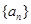
满足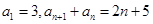
.
（1）求
的表达式；
（2）令
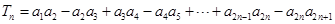,求
.