已知椭圆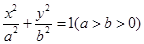
的由顶点为A，右焦点为F，直线
与x轴交于点B且与直线
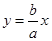交于点C，点O为坐标原点，
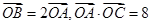,过点F的直线
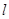与椭圆交于不同的两点M,N.
（1）求椭圆的方程；
（2）求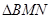
的面积的最大值.
在△ABC中，角A，B，C的对边分别为a，b，c，C＝
，a＝5，△ABC的面积为10
.
(1)求b，c的值；
(2)求cos
的值．
在锐角△ABC中，内角A、B、C的对边分别为a、b、c，且2asinB＝
b.
(1)求角A的大小；
(2)若a＝6，b＋c＝8，求△ABC的面积．
已知函数f(x)＝sin(ωx＋φ)(ω>0，0≤φ≤π)为偶函数，且其图象上相邻两对称轴之间的距离为π.
(1)求函数f(x)的表达式；
(2)若sinα＋f(α)＝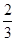
，求
的值．
已知函数f(x)＝Asin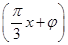
，x∈R，A>0，0<φ<
，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．
(1)求f(x)的最小正周期及φ的值；
(2)若点R的坐标为(1，0)，∠PRQ＝
，求A的值．
已知sin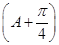
＝
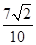，A∈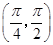
.
(1)求cosA的值；
(2)求函数f(x)＝cos2x＋
sinAsinx的值域．