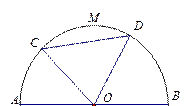
(本小题满分13分)某园林公司计划在一块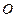 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形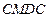 区域用于观赏样板地,
区域用于观赏样板地,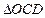 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设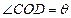 ,
,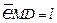 ,分别用
,分别用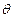 ,
,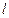 表示弓形
表示弓形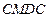 的面积
的面积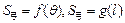 ;
;



|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式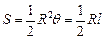 )
)
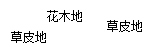 |
在各项均为负数的数列 中,已知点
中,已知点 在函数
在函数 的图像上,且
的图像上,且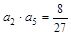 .
.
(Ⅰ)求证:数列 是等比数列,并求出其通项;
是等比数列,并求出其通项;
(Ⅱ)若数列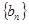 的前
的前 项和为
项和为 ,且
,且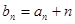 ,求
,求 .
.
某厂家拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令 表示该公司的资助总额.
表示该公司的资助总额.
(Ⅰ)写出 的分布列;
的分布列;
(Ⅱ)求数学期望 .
.
△ABC中,a,b,c分别是角A,B,C的对边,向量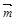 =(2sinB,2-cos2B),
=(2sinB,2-cos2B),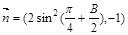 ,
,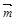 ⊥
⊥ .
.
(Ⅰ)求角B的大小;
(Ⅱ)若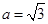 ,b=1,求c的值.
,b=1,求c的值.
已知数列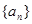 的前n项和为
的前n项和为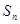 ,且满足
,且满足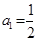 ,
,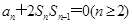 .
.
(Ⅰ)问:数列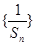 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(Ⅱ)求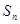 和
和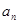 ;
;
(Ⅲ)求证: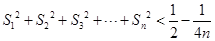 .
.
过抛物线

 的对称轴上的定点
的对称轴上的定点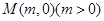 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.