过抛物线

 的对称轴上的定点
的对称轴上的定点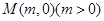 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
已知函数 .
.
(1)求函数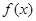 的对称轴方程和单调递增区间;
的对称轴方程和单调递增区间;
(2)若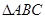 中,
中,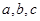 分别是角
分别是角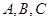 的对边,且
的对边,且 ,
,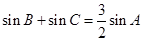 ,求
,求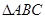 的面积.
的面积.
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求 的极值;
的极值;
(Ⅱ)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,
(Ⅰ)求数列 的前三项
的前三项 ;
;
(Ⅱ)猜想数列 的通项公式
的通项公式 ,并用数学归纳法证明
,并用数学归纳法证明
将边长为 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
已知a、b、c成等差数列且公差 ,求证:
,求证: 、
、 、
、 不可能成等差数列
不可能成等差数列