(本小题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 |
 |
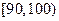 |
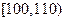 |
 |
 |
| 频数 |
4 |
20 |
15 |
10 |
1 |
乙班
| 成绩 |
 |
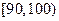 |
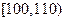 |
 |
 |
| 频数 |
1 |
11 |
23 |
13 |
2 |
(Ⅰ)现从甲班成绩位于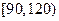 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(Ⅱ)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(Ⅲ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
| |
成绩小于100分 |
成绩不小于100分 |
合计 |
| 甲班 |
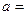 |
26 |
50 |
| 乙班 |
12 |
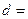 |
50 |
| 合计 |
36 |
64 |
100 |
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
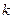 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

已知数列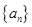 的前
的前 项和为
项和为 ,且
,且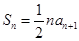 (
( N*),其中
N*),其中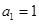 .
.
(Ⅰ) 求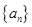 的通项公式;
的通项公式;
(Ⅱ) 设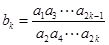 (
( N*).
N*).
①证明:  ;
;
② 求证: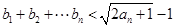 .
.
已知各项都不为零的数列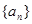 的前n项和为
的前n项和为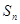 ,
, ,向量
,向量 ,其中
,其中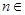 N*,且
N*,且 ∥
∥ .
.
(Ⅰ)求数列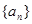 的通项公式及
的通项公式及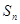 ;
;
(Ⅱ)若数列 的前n项和为
的前n项和为 ,且
,且 (其中
(其中 是首项
是首项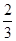 ,第四项为
,第四项为 的等比数列的公比),求证:
的等比数列的公比),求证: .
.
汕头二中拟建一座长 米,宽
米,宽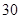 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米(
米(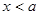 ,
, 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费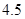 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
已知点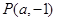 (
(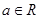 ),过点
),过点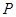 作抛物线
作抛物线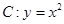 的切线,切点分别为
的切线,切点分别为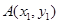 、
、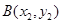 (其中
(其中 ).
).
(Ⅰ)若 ,求
,求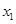 与
与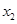 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点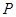 为圆心的圆
为圆心的圆 与直线
与直线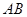 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线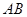 的方程是
的方程是 ,且以点
,且以点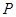 为圆心的圆
为圆心的圆 与直线
与直线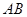 相切,
相切,
求圆 面积的最小值.
面积的最小值.
如图所示的长方体 中,底面
中,底面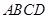 是边长为
是边长为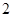 的正方形,
的正方形,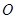 为
为 与
与 的交点,
的交点,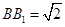 ,
,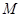 是线段
是线段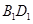 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.