（本小题满分13分）
甲、乙两公司同时开发同一种新产品，经测算，对于函数
，
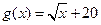，当甲公司投入
万元作宣传时，若乙公司投入的宣传费小于
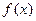万元，则乙公司对这一新产品的开发有失败的风险，否则没有失败的风险；当乙公
司投入万元作宣传时，若甲公司投入的宣传费小于
万元，则甲公司对这一新产品的开发有失败的风险，否则没有失败的风险．
（1）当甲公司不投入宣传费时，乙公司要避免新产品的开发有失败风险，至少要投入多少万元宣传费？
（2）若甲、乙公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能少地投入宣传
费用，问甲、乙两公司应投入多少宣传费？
已知曲线
（
为参数），曲线
，将
的横坐标伸长为原来的2倍，纵坐标缩短为原来的
得到曲线
.
（1）求曲线的普通方程，曲线
的直角坐标方程；
（2）若点P为曲线上的任意一点，Q为曲线上的任意一点，求线段
的最小值，并求此时的P的坐标．
如图，在
中，
是的∠A的平分线，圆
经过点
与
切于点
，与
相交于
，连结
,
．
（1）求证：
；（2）求证：
.
已知函数
.
（1）讨论函数
在
上的单调性；
（2）当
时，曲线
上总存在相异两点，
，
，使得曲线在
、
处的切线互相平行，求证：
.
设椭圆C1：
=1（a＞b＞0）的左、右焦点分别为为
，
恰是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且｜MF2｜=
．
（1）求C1的方程；
（2）平面上的点N满足
，直线l∥MN，且与C1交于A，B两点，若
，求直线l的方程．
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛，其得分情况如茎叶图所示：
（1）若从甲运动员的不低于80且不高于90的得分中任选3个，求其中与平均得分之差的绝对值不超过2的概率；
（2）若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个，求甲、乙两名运动员得分之差的绝对值
的分布列与期望.