本题共2个小题,第1小题6分,第2小题6分.
已知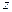 是复数,
是复数,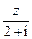 为实数(
为实数(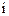 为
为 虚数单位),且
虚数单位),且 .
.
(1)求复数 ;
;
(2)若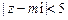 ,求实数
,求实数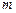 的取值范围.
的取值范围.
.已知:2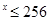 且log
且log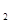
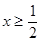 ,
,
(1)求x的取值范围;
(2)求函数f(x)= log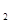 (
( )
)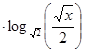 的最大值和最小值。
的最大值和最小值。
已知f(x)是定义在(0,+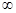 )上的增函数,且满足f(x y)=f(x)+f(y),f(2)=1。
)上的增函数,且满足f(x y)=f(x)+f(y),f(2)=1。
(1)求f(8)
( 2)求不等式f(x)-f(x-2)>3的解集
2)求不等式f(x)-f(x-2)>3的解集
已知集合A=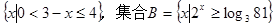 ,求A
,求A 。
。
(文)如图,|AB |=2,O为AB中点,直线
|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线
交于点C,点M在线
段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为锐角三角形时t的取值范围。
(理)已 知数列{an}的前n项和
知数列{an}的前n项和 ,且
,且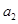 =1,
=1,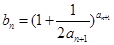
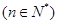 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1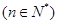 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.