( 本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知 ,
, ,
, 为△ABC的三个内角,向量
为△ABC的三个内角,向量 ,
, ,且
,且 .
.
(1)求 的大小;
的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
在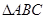 中,角
中,角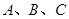 所对的边分别为
所对的边分别为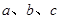 ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若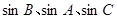 成等比数列,试判断
成等比数列,试判断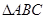 的形状.
的形状.
已知等差数列 的前
的前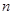 项和为
项和为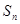 ,且
,且 ,
, ,在等比数列
,在等比数列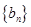 中,
中,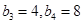 ,
,
(1)求 及
及 ;
;
(2)设数列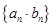 的前
的前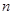 项和
项和 ,求
,求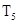
已知直线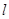

(1)若直线的斜率小于2,求实数 的取值范围;
的取值范围;
(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷2次,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(提示:点到直线的距离公式: )
)
(2)将a,b,5的值分别作为三条线段的长,求这三条线段围成等腰三角形的概率.
下面是计算应纳税所得额的算法过程,其算法如下:
第一步输入工资x(注x<=5000);
第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
否则 y=25+0.1(x-1300)
第三步输出税款y, 结束.
请写出该算法的程序框图.