(本小题满分13分)
已知定义在R上的函数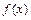 满足:①对任意的
满足:①对任意的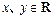 ,都有
,都有 ;②当
;②当 时,有
时,有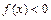 .
.
(1)利用奇偶性的定义,判断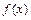 的奇偶性;
的奇偶性;
(2)利用单调性的定义,判断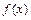 的单调性;
的单调性;
(3)若关于x的不等式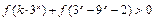 在
在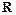 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
已知函数 ,
, .
.
(1)设 是函数
是函数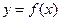 图象的一条对称轴,求
图象的一条对称轴,求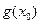 的值;
的值;
(2)求函数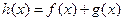 的单调递增区间.
的单调递增区间.
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线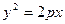 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程. 
将圆x2 + y2 + 2x – 2y = 0按向量a= (1,–1)平移得到圆O,直线l和圆O相交于A、B两点,若在圆O上存在点C,使 ,且
,且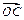 =
= a.
a.
(1)求 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.
如图,四棱锥S—ABCD的底面是边长为1的正方形,
SD垂直于底面ABCD,SB= .
.
(1)求证BC SC;
SC;
(2)设棱SA的中点为M,求异面直线DM与SB所成角的大小.
已知ΔABC的三边方程是AB:5x-y-12=0,BC:x+3y+4=0,CA:x-5y+12=0,
求:(1)∠A的正切;(2)BC边上的高所在的直线的方程.