已知数列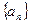
的前
项和为
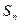，满足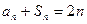
.
（Ⅰ）证明：数列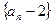
为等比数列，并求出
；
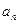（Ⅱ）设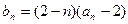
，求
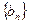的最大项.
已知点P与两个定点O(0,0),A(-3,0)距离之比为
.
(1)求点P的轨迹C方程；
(2)求过点M(2,3)且被轨迹C截得的线段长为2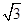
的直线方程．
如图，在直三棱柱ABC-A1B1C1中，底面为等腰直角三角形，AC⊥BC，点D是AB的中点，侧面BB1C1C是正方形．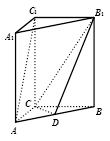
(1) 求证AC⊥B1C；(2)求二面角B-CD-B1平面角的正切值．
已知直线l经过A,B两点，且A(2,1)，
=(4,2).
(1)求直线l的方程；
(2)圆C的圆心在直线l上，并且与x轴相切于(2,0)点，求圆C的方程．
已知奇函数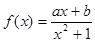
在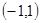
上是增函数，且
① 确定函数
的解析式；
② 解不等式
＜0.
已知函数
的递增区间是
① 求
的值。
② 设
，求
在区间
上的最大值和最小值。