((本小题满分12分)
已知点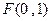 ,一动圆过点
,一动圆过点 且与圆
且与圆 内切.
内切.
(1)求动圆圆心的轨迹 的方程;
的方程;
(2)设点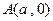 ,点
,点 为曲线
为曲线 上
上 任一点,求点
任一点,求点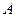 到点
到点 距离的最大值
距离的最大值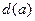 ;
;
(3)在 的条件下,设△
的条件下,设△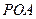 的面积为
的面积为 (
( 是坐标原点,
是坐标原点, 是曲线
是曲线 上横坐标为
上横坐标为 的点),以
的点),以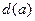 为边长的正方形的面积为
为边长的正方形的面积为 .若正数
.若正数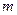 使得
使得 恒成立,问
恒成立,问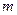 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
已知 在
在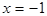 时有极值0。
时有极值0。
(1)求常数 a,b的值;
(2)求f(x)的单调区间。
(3)方程f(x)=c在区间[-4,0]上有三个不同的实根时实数 的范围。
的范围。
在数列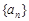 中,已知
中,已知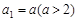 ,且
,且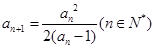 。
。
(1)用数学归纳法证明: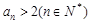 ;
;
(2)求证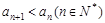 .
.
根据某校五年发展规划,学校将修建一座长 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
已知 的展开式的前三项的系数成等差数列;
的展开式的前三项的系数成等差数列;
(1)求 展开式中所有的有理项;
展开式中所有的有理项;
(2)求 展开式中系数的绝对值最大的项。
展开式中系数的绝对值最大的项。
已知函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数 在
在 上的最大值和最小值.
上的最大值和最小值.