（本小题满分13分）已知抛物线C的顶点为O（0,0），焦点为F（0,1）．
（1）求抛物线C的方程；
（2）过点F作直线交抛物线C于A，B两点．若直线AO，BO分别交直线l：y＝x－2于M，N两点，求|MN|的最小值．
下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料（单位：厘米）：
| 分组 |
人数 |
频率 |
| [122，126) |
5 |
0．042 |
| [126，130) |
8 |
0．067 |
| [130，134 ) |
10 |
0．083 |
| [134，138) |
22 |
0．183 |
| [138，142) |
y |
|
| [142，146) |
20 |
0．167 |
| [146，150) |
11 |
0．092 |
| [150，154) |
x |
0．050 |
| [154，158) |
5 |
0．042 |
| 合计 |
120 |
1．00 |
（1）在这个问题中，总体是什么？并求出x与y的值；
（2）求表中x与y的值，画出频率分布直方图及频率分布折线图；
（3）试计算身高在146~154cm的总人数约有多少？
根据以下算法的程序，画出其相应的算法程图，并指明该算法的目的及输出结果．
n=1
S=0
Do
S=S+n
n=n+1
Loop while S 
2010
输出n-1
某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表：
| x |
3 |
5 |
2 |
7 |
8 |
11 |
| y |
4 |
6 |
3 |
9 |
12 |
14 |
则回归直线方程是_______________．
注：线性回归直线方程系数公式： 
，a=y-bx
在直角坐标系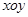
中，以O为圆心的圆与直线
相切.
（1）求圆O的方程；
（2）圆O与
轴相交于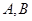
两点，圆内的动点
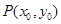满足
，
求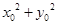
的取值范围.
如图，四棱锥P －ABCD的底面是矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD，E 为侧棱PD的中点。
（1）证明：PB//平面EAC；
（2）若AD="2AB=2," 求直线PB与平面ABCD所成角的正切值；