(本小题满分12分)
某校高二年级共有1200名学生,为了分析某一次数学考试情况,今抽查100份试卷,成绩分布如下表:
| 成绩 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 人数 |
4 |
5 |
6 |
9 |
21 |
27 |
15 |
9 |
4 |
| 频率 |
0.04 |
0.05 |
0.06 |
0.09 |
0.21 |
0.27 |
0.15 |
0.09 |
0.04 |
(Ⅰ)画出频率分布直方图;
 |
 |
(Ⅱ)由频率分布表估计这次考试及格(60分以上为及格)的人数;
(Ⅲ)由频率分布直方图估计这考试的平均分.
选修4-5:不等式选讲
关于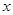 的不等式
的不等式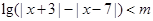 .
.
(1)当 时,解此不等式;
时,解此不等式;
(2)设函数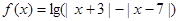 ,当
,当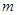 为何值时,
为何值时, 恒成立?
恒成立?
选修4-4:坐标系与参数方程
已知直线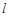 的参数方程是
的参数方程是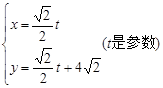 ,圆C的极坐标方程为
,圆C的极坐标方程为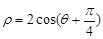 .
.
(1)求圆心C的直角坐标;
(2)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
选修4-1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.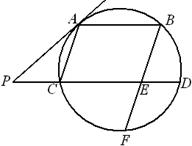
已知函数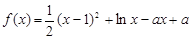 .
.
(1)若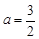 ,求函数
,求函数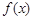 的极值;
的极值;
(2)若对任意的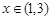 ,都有
,都有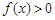 成立,求
成立,求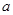 的取值范围.
的取值范围.
抛物线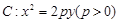 上一点
上一点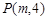 到其焦点的距离为5.
到其焦点的距离为5.
(1)求 与
与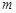 的值;
的值;
(2)若直线 与抛物线
与抛物线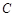 相交于
相交于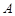 、
、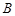 两点,
两点,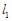 、
、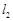 分别是该抛物线在
分别是该抛物线在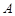 、
、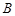 两点处的切线,
两点处的切线,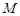 、
、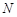 分别是
分别是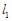 、
、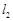 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证: