(1) 解方程:
(2)解方程: .
.
如图,把一张边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒,求纸盒的四个侧面的面积之和(结果用关于x、y的代数式表示).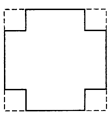
先化简,再求值:6x2-(2x+1)(3x-2)+(x+3)(x-3),其中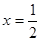
作图题: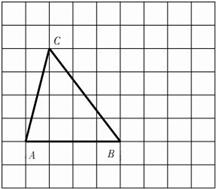
(1)在单位长度为1方格纸中,将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.
(2)求△A1B1C1的面积
计算:(1)2a2b·3ab2(2)3x(x2-2x-1)
(3)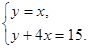 (4)
(4)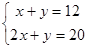
大约1500年以前,我国古代数学家张丘建在他编写的《张丘建算经》里,曾经提出并解决了“百钱买百鸡”这个有名的数学问题,通俗地讲就是下例:
今有公鸡每只五个钱,母鸡每只三个钱,小鸡每个钱三只.用100个钱买100只鸡,问公鸡、母鸡、小鸡各买了多少只?