:已知数列 的前n项和为
的前n项和为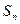 满足
满足 ,
,
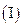 猜想数列
猜想数列 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅱ) 对于数列 若存在常数M>0,对任意的
若存在常数M>0,对任意的 ,恒有
,恒有

 ,, 则称数列
,, 则称数列 为B-数列。问数列
为B-数列。问数列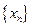 是B-数列吗? 并证明你的结论。
是B-数列吗? 并证明你的结论。
(本小题共13分)
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5.甲先摸出一个球,记下编号为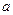 ,放回袋中后,乙再摸一个球,记下编号为
,放回袋中后,乙再摸一个球,记下编号为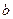 .
.
(Ⅰ)求“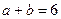 ”的事件发生的概率;
”的事件发生的概率;
(Ⅱ)若点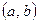 落在圆
落在圆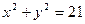 内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
内,则甲赢,否则算乙赢,这个游戏规则公平吗?试说明理由.
(本小题共13分)
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的体积;
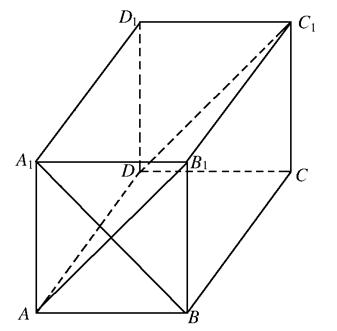
(Ⅱ)若组合体的底部几何体记为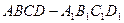 ,其中
,其中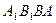 为正方形.
为正方形.
(i)求证: ;
;
(ii)求证: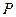 为棱
为棱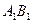 上一点,求
上一点,求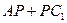 的最小值.
的最小值.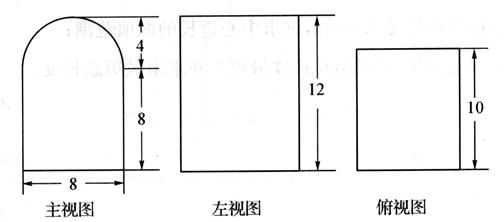
(本小题共13分)
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30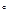 ,相距10海里C处的乙船.
,相距10海里C处的乙船.
(Ⅰ)求处于C处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线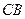 方向前往
方向前往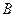 处救援,其方向与
处救援,其方向与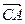 成
成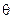 角,
角,
求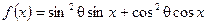 (x∈
(x∈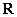 )的值域.
)的值域.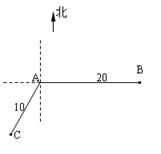
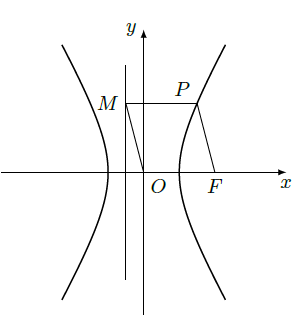
如图, 为双曲线 : 的右焦点。 为双曲线 右支上一点,且位于 轴上方, 为左准线上一点, 为坐标原点。已知四边形 为平行四边形, .
(Ⅰ)写出双曲线
的离心率
与
的关系式;
(Ⅱ)当
时,经过焦点
且品行于
的直线交双曲线于
、
点,若
,求此时的双曲线方程.
数列 的前 项和为 ,已知
(Ⅰ)写出 与 的递推关系式 ,并求 关于 的表达式;
(Ⅱ)设 ,求数列 的前 项和 .