(本小题满分14分)
已知F1,F2分别是椭圆+=1的左、右焦点,曲线C是以坐标原点为顶点,以F2为焦点的抛物线,自点F1引直线交曲线C于P、Q两个不同的交点,点P关于x轴的对称点记为M.设=λ.
(Ⅰ)求曲线C的方程;
(Ⅱ)证明:=-λ;
(Ⅲ)若λ∈[2,3],求|PQ|的取值范围.
已知:复数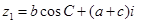 ,
,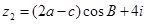 ,且
,且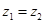 ,其中
,其中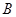 、
、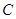 为△ABC的内角,
为△ABC的内角,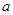 、
、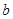 、
、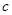 为角
为角 、
、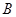 、
、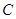 所对的边.
所对的边.
(1)求角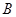 的大小;
的大小;
(2)若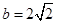 ,求△ABC的面积.
,求△ABC的面积.
已知函数
(1)若 在
在 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(2)若 在
在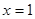 处取得极值,且
处取得极值,且 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,设A是单位圆和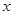 轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且
轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且 ,
, .
.
(1)若点Q的坐标是 ,求
,求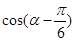 的值;
的值;
(2)设函数 ,求
,求 的值域.
的值域.
已知命题 :关于
:关于 的不等式
的不等式 对一切
对一切 恒成立;命题
恒成立;命题 :函数
:函数 在
在 上递减.若
上递减.若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
(1)学校规定:成绩不低于75分的为优秀.请画出下面的 列联表.
列联表.
| 甲班 |
乙班 |
合计 |
|
| 优秀 |
|||
| 不优秀 |
|||
| 合计 |
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式: