袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个,从中每次任取1个.有放回地抽取3次,求:
(1)3个全是红球的概率. (2)3个颜色全相同的概率.
(3)3个颜色不全相同的概率. (4)3个颜色全不相同的概率.
已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.
如图,在△OAB中,已知P为线段AB上的一点,且|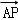 |=2|
|=2| |.
|.
(Ⅰ)试用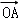 ,
, 表示
表示 ;
;
(Ⅱ)若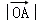 =3,
=3,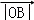 =2,且∠AOB=60°,求
=2,且∠AOB=60°,求 •
•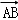 的值.
的值.
已知
,且
是第一象限.
(1)求
的值;
(2)求
的值.
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn= ,证明:数列{bn}是等差数列;
,证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn,
(3)设cn= ,求数列{cn}的最大项.
,求数列{cn}的最大项.