.(本题满分15分)
已知四点 ,
, ,
, ,
, 。点
。点 在抛物线
在抛物线 上
上
(Ⅰ) 当 时,延长
时,延长 交抛物线于另一点
交抛物线于另一点 ,求
,求 的大小;
的大小;
(Ⅱ)当点
 在抛物线
在抛物线 上运动时,
上运动时,
ⅰ)以 为直径作圆,求该圆截直线
为直径作圆,求该圆截直线 所得的弦长;
所得的弦长;
ⅱ)过点 作
作 轴的垂线交
轴的垂线交 轴于点
轴于点 ,过点
,过点 作该抛物线的切线
作该抛物线的切线 交
交 轴于点
轴于点 。问:是否总有
。问:是否总有 ?如果有,请给予证明;如果没有,请举出反例。
?如果有,请给予证明;如果没有,请举出反例。
(本小题满分8分)
(1)已知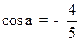 ,且
,且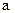 为第三象限角,求
为第三象限角,求 的值
的值
(2)已知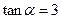 ,计算
,计算 的值
的值
(本小题满分14分)
已知动圆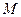 过定点
过定点 ,且与定直线
,且与定直线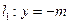 相切,动圆圆心
相切,动圆圆心
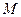 的轨迹为
的轨迹为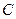 ,直线
,直线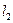 过点
过点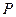 交曲线
交曲线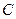 于
于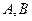 两点.
两点.
(Ⅰ)求曲线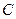 的方程;
的方程;
(Ⅱ)若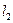 交
交 轴于点
轴于点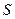 ,且
,且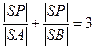 ,求
,求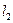 的方程;
的方程;
(Ⅲ)若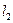 的倾斜角为
的倾斜角为 ,在
,在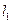 上是否存在点
上是否存在点 使
使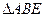 为正三角形? 若能,求点
为正三角形? 若能,求点 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
(本小题满分12分)
已知函数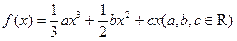 在点
在点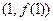 处的切线斜率为
处的切线斜率为 ,且
,且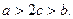
(Ⅰ)证明: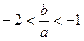 ; (Ⅱ)证明:函数
; (Ⅱ)证明:函数 在区间
在区间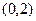 内至少有一个极值点.
内至少有一个极值点.
(本小题满分12分)
已知函数 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式及
的通项公式及 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中 ,求
,求 的前
的前 项和.
项和.
(本小题满分12分)
如图1,直角梯形 中,
中, ,
, 分别为边
分别为边 和
和 上的点,且
上的点,且 ,
, .将四边形
.将四边形 沿
沿 折起成如图2的位置,使
折起成如图2的位置,使 .
.
(Ⅰ)求证:
 平面
平面 ;
;
(Ⅱ)求四棱锥 的体积;
的体积;
(Ⅲ)求面 与面
与面 所成锐二面角的余弦值.
所成锐二面角的余弦值.