如图一,在△ABC中,分别以AB,AC为直径在△ABC外作半圆 和半圆
和半圆 ,其中
,其中 和
和 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 
(1)连结 ,证明:
,证明: ;
;
(2)如图二,过点A分别作半圆 和半圆
和半圆 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
(3)如图三,过点A作半圆 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线
的切线
(年云南省昆明市)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)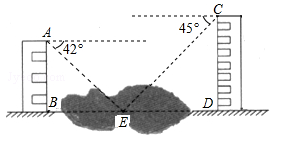
(年云南省)为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: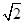 ≈1.41,
≈1.41,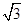 ≈1.73,结果保留整数)
≈1.73,结果保留整数)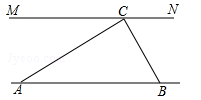
(年云南省昆明市)如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.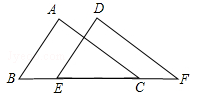
(年云南省)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.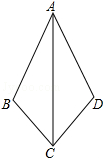
(年贵州省贵阳市)在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.