((本小题满分13分)
已知椭圆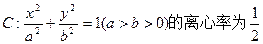 ,以原点为圆心,椭
,以原点为圆心,椭 圆的短半轴为半径的圆与直线
圆的短半轴为半径的圆与直线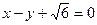 相切。
相切。
(1)求椭圆C的方程;
(2)设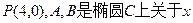 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结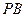 交椭圆
交椭圆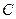
于另一点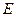 ,证明:直线
,证明:直线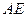 与x轴相交于定点
与x轴相交于定点
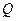 ;
;
(3) 在(2)的条件下,过点
在(2)的条件下,过点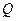 的直线与椭圆
的直线与椭圆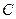 交于
交于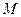 、
、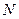 两点,求
两点,求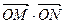 的取值
的取值
范围。
平面内与两定点 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数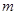 的点的轨迹,加上
的点的轨迹,加上 两点,所成的曲线
两点,所成的曲线 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(Ⅰ)求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与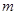 值的关系;
值的关系;
(Ⅱ)当 时,对应的曲线为
时,对应的曲线为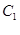 ;对给定的
;对给定的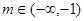 ,对应的曲线为
,对应的曲线为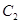 ,若曲线
,若曲线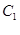 的斜率为
的斜率为 的切线与曲线
的切线与曲线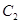 相交于
相交于 两点,且
两点,且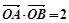 (
( 为坐标原点),求曲线
为坐标原点),求曲线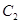 的方程.
的方程.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,
PA=BC=1,PD=AB=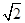 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.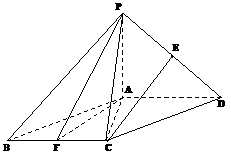
(Ⅰ) 求证:CE∥平面PAF;
(Ⅱ)在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于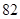 为正品,小于
为正品,小于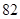 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各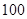 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 |
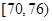 |
 |
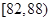 |
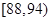 |
 |
| 元件A |
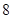 |
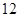 |
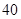 |
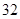 |
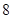 |
| 元件B |
 |
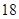 |
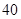 |
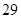 |
 |
(Ⅰ)试分别估计元件A,元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
在公比为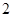 的等比数列
的等比数列 中,
中,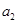 与
与 的等差中项是
的等差中项是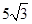 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数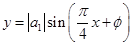 ,
,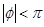 ,的一部分图像如图所示,
,的一部分图像如图所示, ,
, 为图像上的两点,设
为图像上的两点,设 ,其中
,其中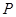 与坐标原点
与坐标原点 重合,
重合,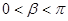 ,求
,求 的值.
的值.
已知数列 ,
, 满足:
满足: .
.
(1)若 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 ,且
,且 .
.
① 记 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
② 若数列 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项 应满足的条件.
应满足的条件.