(本小题满分12分)
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用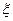 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出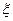 的分布列,并求
的分布列,并求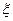 的数学期望。
的数学期望。
对于函数  ,若存在
,若存在 ,使
,使  成立,则称
成立,则称 为
为 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) =  .
.
(I)试问 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列 的各项均为负数,且满足
的各项均为负数,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(III)已知 ,求
,求 的前项和
的前项和 .
.
a11,a12,……a18
a21,a22,……a28
……………………
64个正数排成8行8列, 如下所示: a81,a82,……a88
在符合 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且 ,
, ,
, 。
。
⑴若 ,求
,求 和
和 的值。
的值。
⑵记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足 ,联
,联 (m为非零常数),
(m为非零常数), ,且
,且 ,求
,求 的取值范围。
的取值范围。
⑶对⑵中的 ,记
,记 ,设
,设 ,求数列
,求数列 中最大项的项数。
中最大项的项数。
已知函数f(x)=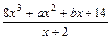 ,定义域为[-1,1]
,定义域为[-1,1]
(Ⅰ)若a=b=0,求f(x)的最小值; (Ⅱ)若对任意x∈[-1,1],不等式6≤f(x)≤5+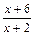 均成立,求实数a,b的值.
均成立,求实数a,b的值.
设 =
= (a>0)为奇函数,且
(a>0)为奇函数,且 min=
min= ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 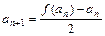 ,
,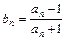 .
.
(1)求f(x)的解析表达式; (2) 证明:当n∈N+时, 有bn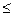
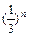 .
.
设函数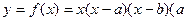 、
、 R)。
R)。
(1)若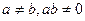 ,过两点(0,0)、(
,过两点(0,0)、( ,0)的中点作与
,0)的中点作与 轴垂直的直线,与函数
轴垂直的直线,与函数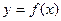 的图象交于点
的图象交于点 ,求证:函数
,求证:函数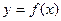 在点P处的切线点为(
在点P处的切线点为( ,0)。
,0)。
(2)若 ),且当
),且当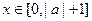 时
时 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。