如图所示,椭圆 与直线
与直线 相切于点
相切于点 .
.
(1)求 满足的关系式,并用
满足的关系式,并用 表示点
表示点 的坐标;
的坐标;
(2)设 是椭圆的右焦点,若
是椭圆的右焦点,若 是以
是以 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆 的标准方程.
的标准方程.
(本小题12分)
有两颗正四面体的玩具,其四个面上分别标有数字1,2,3,4,下面做投掷这两颗正四面体玩具的试验 :用
:用 表示结果,其中
表示结果,其中 表示投掷第1颗正四面体玩具落在底面的数字,
表示投掷第1颗正四面体玩具落在底面的数字, 表示投掷第2颗正四面体玩具落在底面的数字。
表示投掷第2颗正四面体玩具落在底面的数字。
(1)写出试验的基本事件; (2)求事件“落在底面的数字之和大于3”的概率;
(2)求事件“落在底面的数字之和大于3”的概率;
(3)求事件“落在底面的数字相等”的概率。
已知数列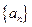 的前
的前 项和为
项和为
(1)求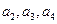 的值;
的值;
(2)求数列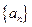 的通项公式;
的通项公式;
(3)设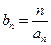 ,求证:数列
,求证:数列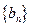 的前
的前 项和
项和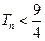 。
。
在 中,已知内角A、B、C成等差数列,边AC
中,已知内角A、B、C成等差数列,边AC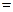 6。设内角
6。设内角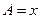 ,
, 的周长为
的周长为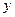 。
。
如图,B、A是某海面上位于东西方向相距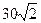 海里的两个观测点。现位于B点正北方向、A点北
海里的两个观测点。现位于B点正北方向、A点北 偏东
偏东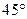 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西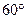 、A点北偏西
、A点北偏西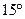 的
的 D点的救援船立即前往营救,其航行速度为
D点的救援船立即前往营救,其航行速度为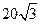 海里/小时。问该救援船到达C点需要多少时间?
海里/小时。问该救援船到达C点需要多少时间?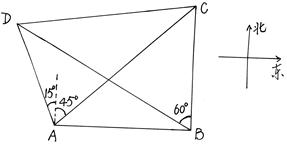
.(12分)
设等差数列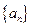 的前
的前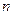 项和为
项和为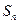 ,已知
,已知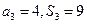 。
。
(1)求数列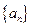 的通项公式;
的通项公式;
(2)令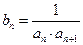 ,求数列
,求数列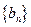 的前10项和。
的前10项和。