如图,已知直角梯形 的上底
的上底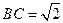 ,
,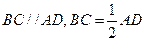 ,
,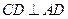 ,平面
,平面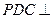 平面
平面 ,
,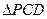 是边长为
是边长为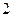 的等边三角形。
的等边三角形。
(1)证明: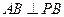 ;
;
(2)求二面角 的大小。
的大小。
(3)求三棱锥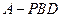 的体积。
的体积。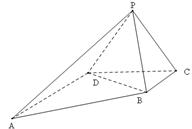
已知椭圆 +
+ =1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
=1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
设椭圆的中心为坐标原点,它在x轴上的一个焦点与短轴两端点连成60°的角,两准线间的距离等于8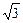 ,求椭圆方程.
,求椭圆方程.
如下图,已知△OFQ的面积为S,且 ·
· =1,
=1,
(1)若S的范围为 <S<2,求向量
<S<2,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设| |=c(c≥2),S=
|=c(c≥2),S= c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当| |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
已知双曲线x2- =1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.
=1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.
(1)求线段P1P2的中点P的轨迹方程;
(2)过点B(1,1)能否作直线l′,使l′与已知双曲线交于两点Q1、Q2,且B是线段Q1Q2的中点?请说明理由.
已知椭圆的两焦点为F1(0,-1)、F2(0,1),直线y=4是椭圆的一条准线.
(1)求椭圆方程;
(2)设点P在椭圆上,且|PF1|-|PF2|=1,求tan∠F1PF2的值.