（本小题满分13分）
某奖励基金发放方式为：每年一次，把奖金总额平均分成6份，奖励在某6个方面为人类作出最有益贡献的人，每年发放奖金的总金额是基金在该年度所获利息的一半，另一半利息存入基金总额，以便保证奖金数逐年增加。假设基金平均年利率为
，2000年该奖发放后基金总额约为21000万元。用
表示为第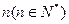
年该奖发放后的基金总额（2000年为第一年）。
（1）用
表示
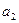与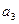
，并根据所求结果归纳出的表达式；
（2）试根据的表达式判断2011年度该奖各项奖金是否超过150万元？并计算从2001年到2011年该奖金累计发放的总额。
（参考数据：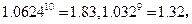
）
（本小题满分13分）已知函数
的反函数为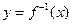
，定义：若对给定的实数
，函数
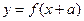与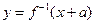
互为反函数，则称满足“和性质”．（1）判断函数
是否满足“1和性质”，并说明理由；（2）若
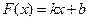，其中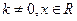
满足“2和性质”，则是否存在实数a，使得
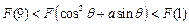对任意的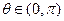
恒成立？若存在，求出的范围；若不存在，请说明理由．
（本小题满分12分）若关于的实系数方程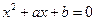
有两个根，一个根在区间
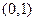内，另一根在区间
内，记点
对应的区域为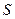
．（1）设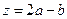
，求的取值范围；（2）过点
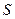的一束光线，射到轴被反射后经过区域，求反射光线所在直线
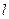经过区域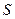内的整点（即横纵坐标为整数的点）时直线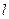的方程．
设有半径为3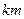
的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3：1，问两人在何处相遇？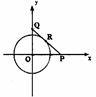
如图2，圆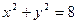
内有一点
，
为过点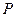
且倾斜角为
的弦，当
＝135０时，求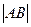
;当弦
被点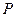平分时，求出直线的方程; 设过
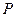点的弦的中点为
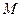，求点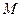的坐标所满足的关系式. 
图2
．已知一曲线是与两个定点
、
距离的比为
的点的轨迹，则求此曲线的方程.