（本小题满分12分）
如图，在四棱锥P－ABCD中，底面为正文形，PA
平面ABCD，且PA＝AD，E为棱PC上的一点，PD平面ABE
（I）求证：E为PC的中点
（II）若N为CD中点，M为AB上的动点，当直线MN与平面ABE所成的角最大时，求二面角C－EM—N的大小 
（本小题满分12分）点A、B分别是椭圆
长轴的左、右端点，点F是
椭圆的右焦点，点P在椭圆上，且位于
轴上方，
.
（1）求点P的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线A
P的距离等于
，求椭圆上的点到点M的距离
的最小值.
（本小题满分12分）点P到M(-1,0)、N(1,0)的距离之差为2m,到x轴、y轴的距离之比为2.求m的取值范围.
（本小题满分10分）P是椭圆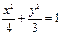
上的点,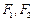 
是椭圆的左右焦点,设
.求
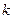的最大值与最小值的差.
（本小题满分12分）平面上有两点A（-1，0），B（1，0），P为圆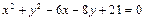
上的一点，试求
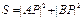的最大值与最小值，并求相应的P点坐标．
（本小题满分12分）已知⊙C：x2＋y2－2x－2y＋1＝0，直线l与⊙C相切且分别交x轴、y轴正向于A、B两点，O为坐标原点，且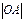
＝a，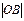
＝b（a＞2，b＞2）．
（Ⅰ）求线段AB中点的轨迹方程.
（Ⅱ）求△ABC面积的极小值．