(本小题满分10分)P是椭圆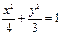 上的点,
上的点, 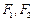 是椭圆的左右焦点,设
是椭圆的左右焦点,设 .求
.求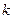 的最大值与最小值的差.
的最大值与最小值的差.
如图,将边长为2,有一个锐角为60°的菱形 ,沿着较短的对角线
,沿着较短的对角线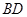 对折,使得
对折,使得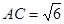 ,
,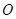 为
为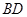 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足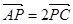 。
。
(Ⅰ)求证: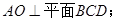
(Ⅱ)求三棱锥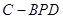 的体积;
的体积;
(Ⅲ)求二面角 的余弦值.
的余弦值.
平面内动点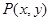 到定点
到定点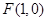 的距离比它到
的距离比它到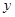 轴的距离大
轴的距离大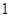 。
。
(1)求动点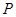 的轨迹
的轨迹 的方程;
的方程;
(2)已知点A(3,2), 求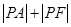 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组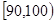 ,第二组
,第二组 ,,第五组
,,第五组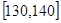 .按上述分组方法得到的频率分布直方图如图所示.
.按上述分组方法得到的频率分布直方图如图所示.
(1)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;
(2)若从第一、五组中共随机取出两个成绩,求这两个成绩差的绝对值大于30分的概率.
命题 : “方程
: “方程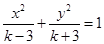 表示双曲线”(
表示双曲线”( );命题
);命题 :
: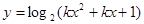 定义域为
定义域为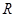 ,若命题
,若命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数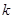 的取值范围.
的取值范围.
已知函数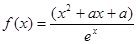 ,(
,(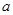 为常数,
为常数,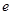 为自然对数的底).
为自然对数的底).
(1)令 ,
, ,求
,求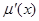 和
和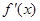 ;
;
(2)若函数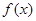 在
在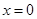 时取得极小值,试确定
时取得极小值,试确定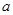 的取值范围;
的取值范围;
(3)在(2)的条件下,设由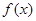 的极大值构成的函数为
的极大值构成的函数为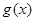 ,试判断曲线
,试判断曲线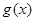 只可能与直线
只可能与直线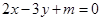 、
、 (
(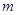 ,
,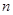 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.