国庆前夕,我国具有自主知识产权的“人甲型H1N1流感病毒核酸检测试剂盒”(简称试剂盒)在上海进行批量生产,这种“试剂盒”不仅成本低操作简单,而且可以准确诊断出“甲流感”病情,为甲型H1N1流感疫情的防控再添一道安全屏障.某医院在得到 “试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做
“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做 了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为
了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为 。
。
(1)求出这5位发热病人中“甲流感”患者 的人数
的人数 ;
;
(2)若用“试剂盒”逐个检测这5位发热病人,直到能确定“甲流感”患者为止,设ξ表示检测次数,求ξ的分布列及数学期望Eξ。
已知函数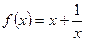
(1) 用函数单调性的定义证明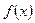 在区间
在区间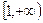 上为增函数
上为增函数
(2) 解不等式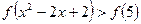
已知集合A=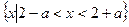 ,
,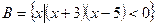
(1) 若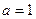 ,求
,求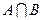
(2) 若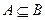 ,求
,求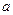 的取值范围
的取值范围
将十天干、十二地支按顺序依次排列,若 表示处于第
表示处于第 个位置的天干或地
个位置的天干或地
支,.
| 十天干 |
十二地支 |
|||||||||||||||||||||
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
 |
甲 |
乙 |
丙 |
丁 |
戊 |
己 |
庚 |
辛 |
壬 |
癸 |
子 |
丑 |
寅 |
卯 |
辰 |
巳 |
午 |
未 |
申 |
酉 |
戌 |
亥 |
如上表,即: ,
, .定义函数
.定义函数 .
.
(1)分别求 ,
, ,
,
(2) 2010年是庚寅年,我们也可以用
 的表示形式来表示该年,求
的表示形式来表示该年,求
的值
(本小题满分13分)已知函数 (
( ).
).
(1)若函数 有三个零点分别为
有三个零点分别为 ,且
,且 ,
, ,求函数
,求函数 的单调区间;
的单调区间;
(2)若 ,
, ,证明:函数
,证明:函数 在区间(0,2)内一定有极值点;
在区间(0,2)内一定有极值点;
(3)在(2)的条件下,若函数 的两个极值点之间的距离不小于
的两个极值点之间的距离不小于 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)已知函数 (
( ).
).
(1)若函数 在
在 处的切线与x轴平行,求a的值,并求出函数的极值;
处的切线与x轴平行,求a的值,并求出函数的极值;
(2)已知函数 ,在(1)的条件下,若
,在(1)的条件下,若 恒成立,求b的取值范围.
恒成立,求b的取值范围.