已知定点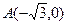 ,B是圆
,B是圆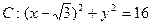 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(1)求动点E的轨迹方程;
(2)设直线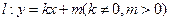 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: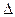 OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线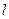 的方程.
的方程.
(本小题满分10分)已知:等差数列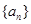 ,
, ,前
,前 项和为
项和为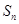 .各项均为正数的等比数列列
.各项均为正数的等比数列列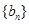 满足:
满足: ,
, ,且
,且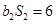 .
.
(1)求数列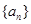 与
与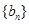 的通项公式;
的通项公式;
(Ⅱ)求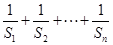
(本小题满分10分) 在 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足

(1)求角 的大小;
的大小;
(2)若 为钝角三角形,求实数
为钝角三角形,求实数 的取值范围。
的取值范围。
(本小题满分13分)
已知二次函数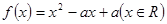 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式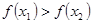 成立.
成立.
设数列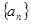 的前
的前 项和
项和 ,
,
(1)求数列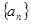 的通项公式;
的通项公式;
(2)数列 中,令
中,令 ,
,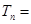
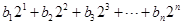 ,求
,求 ;
;
(3)设各项均不为零的数列 中,所有满足
中,所有满足 的正整数
的正整数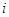 的个数称为这个数列
的个数称为这个数列 的变号数。令
的变号数。令 (
( 为正整数),求数列
为正整数),求数列 的变号数.
的变号数.
(本小题满分13分)
已知抛物线、椭圆和双曲线都经过点 ,它们在
,它们在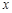 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这三条曲线的方程;
(2)对于抛物线上任意一点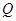 ,点
,点 都满足
都满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分))
京广高铁于2012年12月26日全线开通运营,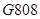 次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程
次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程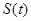 (单位:
(单位: )和时间
)和时间 (单位:
(单位: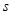 )的关系为:
)的关系为: .
.
(1)求从开始紧急刹车至列车完全停止所经过的时间;
(2)求列车正常行驶的速度;
(3)求紧急刹车后列车加速度绝对值的最大值.