如图,正四棱柱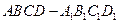 中,
中,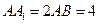 ,点
,点 在
在 上且
上且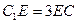 ,点
,点 是线段
是线段 的中点
的中点
(Ⅰ)证明: 平面
平面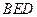 ;
;
(Ⅱ)求二面角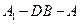 的正切值;
的正切值;
(Ⅲ)求三棱锥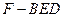 的体积.
的体积.
(本小题满分12分)
已知A、B分别为曲线C: 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
(I)当 ,求点T坐标;
,求点T坐标;
(II)点M在x轴上方,若 的面积为2,当
的面积为2,当 的面积的最大值为
的面积的最大值为 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。
如图,三棱锥S—ABC中,AB⊥BC,D、E分别为AC、BC的中点,SA=SB=SC。
(1)求证:BC⊥平面SDE;
(2)若AB=BC=2,SB=4,求三棱锥S—ABC的体积。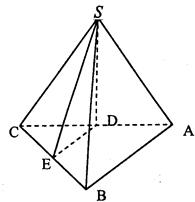
一汽车厂生产A、B、C三类轿车,每类轿车有豪华型和标准型两种型号,某月生产情况如下表(单位:辆)
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
x |
| 标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(I)求x的值;
(I)列出所有基本事件,并求出至少有一辆是豪华型轿车的概率.
在△ABC中,角A、B、C的对边分别为a,b,c,已知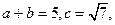 且
且
(I)求角C的大小;
(II)求△ABC的面积。
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.
23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式