(本小题满分13分)
随着国家政策对节能环保型小排量车的调整，两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2010年1月Q型车的销量为a辆，通过分析预测，若以2010年1月为第1月，其后两年内Q型车每月的销量都将以1%的比率增长，而R型车前n个月的销售总量Tn大致满足关系式：Tn＝228a(1.012n－1)(n≤24，n∈N*).
(1)求Q型车前n个月的销售总量Sn的表达式；
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系；
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%，并说明理由.
(参考数据：≈1.09，≈8.66)
（本小题满分12分）设函数
（1）若
；
（2）若
（本小题满分12分）
抛物线的顶点在原点，焦点在x轴的正半轴上，直线x+y-1=0与抛物线相交于A、B两点，且
。
(1) 求抛物线方程；
(2) 在x轴上是否存在一点C,使得三角形ABC是正三角形? 若存在，求出点C的坐标，若不存在，说明理由.
（本小题满分12分）
如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，
BCD=60
，E是CD的中点，PA
底面ABCD，PA=2.
（1）证明：平面PBE平面PAB；
（2）求平面PAD和平面PBE所成二面角的正弦值。
（本小题满分12分）
某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：
.
（1）求图中x的值；
（2）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为
，求的分布列和数学期望。
（本小题满分12分）在数列
中，
，并且对于任意n∈N*，都有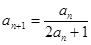
．
（1）证明数列
为等差数列，并求的通项公式；
（2）设数列
的前n项和为
，求使得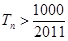
的最小正整数
.